Intro to Grad-CAM - CNN的可视化

The Grad-CAM (Gradient-weighted Class Activation Mapping) is a generalization of CAM and is applicable to a significantly broader range of CNN model families.
The intuition is to expect the last convolutional layers to have the best compromise between high-level semantics and detailed spatial information which is lost in fully-connected layers. The neurons in these layers look for semantic class-specific information in the image.

$$L_{Grad-CAM}^c = ReLU(\sum_k\alpha_k^cA^k)$$

where $$\alpha_k^c = \frac{1}{Z}\sum_i\sum_j\frac{\partial{y_c}}{\partial{A_{ij}^k}}$$

The $L_{Grad-CAM}^c$ is the class-discrimitive localization map for any class c.
And the $\alpha_k^c$ represents a partial linearization of the deep network downstream from A, and captures the ‘importance’ of feature map k for a target class c. The $\frac{1}{Z}\sum_i\sum_j$ stands for the global average pooling.

• We apply a ReLU to the linear combination of maps because we are only interested in the features that have a positive influence on the class of interest, i.e. pixels whose intensity should be increased in order to increase y. Negative pixels are likely to belong to other categories in the image.

• The formula inside the ReLU bracket follows the same principle as the CAM formula, which is to perform a linear summation of the feature maps from the last convolutional layer, weighted accordingly, to obtain the activation map.

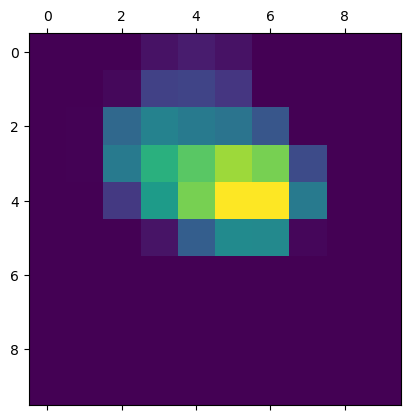
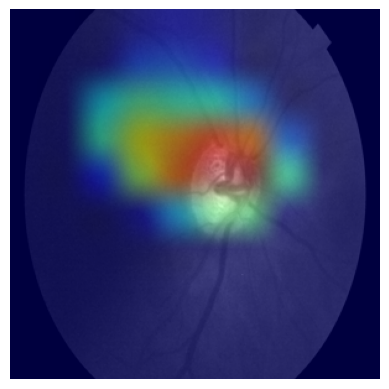
The code below uses the gradients of retinal target flowing into the final convolutional layer to produce a coarse localization map highlighting the important regions in the image for predicting the concept.

The model used in this approach has a following structure:

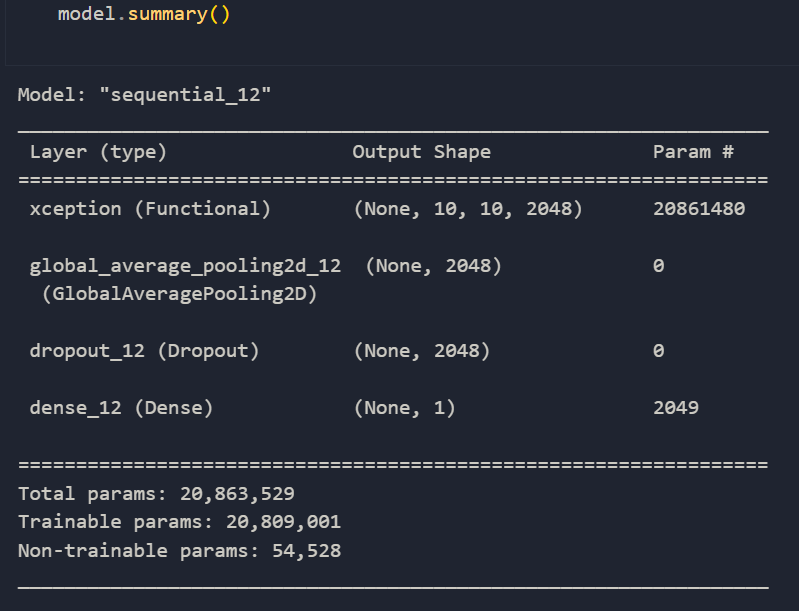
base_model = model.get_layer('xception')
# base_model.summary()

last_conv_layer = base_model.get_layer('block14_sepconv2_act')
last_conv_layer_output = last_conv_layer.output

intermediate_model = Model(inputs=base_model.input, outputs=last_conv_layer_output)

x = intermediate_model.output
x = model.get_layer('global_average_pooling2d_12')(x)
x = model.get_layer('dropout_12')(x)
final_output = model.get_layer('dense_12')(x)
grad_model = Model(inputs=intermediate_model.input, outputs=[last_conv_layer_output, final_output])

# Get the gradient of the top predicted class for the input image with respect to the activations of the last conv layer
with tf.GradientTape() as tape:
    # Forward pass
    last_conv_layer_output, preds = grad_model(img_batch)
    # print(preds) # the preds should be a single value (the predicated age)
    model_output = preds[:, 0]  # Assuming the model outputs a single value for age prediction

# Compute gradients
grads = tape.gradient(model_output, last_conv_layer_output)
# print(grads.shape) # (1, 10, 10, 2048)

# This is a vector where each entry is the mean intensity of the gradient over a specific feature map channel
pooled_grads = tf.reduce_mean(grads, axis=(0, 1, 2))


last_conv_layer_output = last_conv_layer_output[0]
heatmap = last_conv_layer_output @ pooled_grads[..., tf.newaxis]
heatmap = tf.squeeze(heatmap)

# For visualization purpose, we will also normalize the heatmap between 0 & 1
heatmap = tf.maximum(heatmap, 0) / tf.math.reduce_max(heatmap)
# Convert the heatmap to RGB
heatmap = np.uint8(255 * heatmap)

# Apply the heatmap to the original image
jet = mpl.colormaps["jet"]

# Use RGB values of the colormap
jet_colors = jet(np.arange(256))[:, :3]
jet_heatmap = jet_colors[heatmap]

# Create an image with RGB colorized heatmap
jet_heatmap = keras.utils.array_to_img(jet_heatmap)
jet_heatmap = jet_heatmap.resize((img.shape[1], img.shape[0]))
jet_heatmap = keras.utils.img_to_array(jet_heatmap)

superimposed_img = jet_heatmap * 0.002 + img
superimposed_img = keras.utils.array_to_img(superimposed_img)

# Display the image with attention map
plt.imshow(superimposed_img)
plt.axis('off')
plt.show()

References ⭐

• Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization
• paper-code-grad-cam
• keras-grad_cam.py
• pytorch_CAM.py
• 注意力可视化Grad-CAM