Intro to GAN
Supervised or unsupervised?
- Unsupervised task: generative modeling is an unsupervised task where the model is not told what kind of patterns to look for in the data and there is no error metric to improve the model.
- Supervised classifier/loss func: the training process of the GAN is posed as a supervised learning problem with the help of a discriminator.
Generator and Discriminator
In this blog, we will only talk about the vanilla GANs. The core idea that rules GANs is based on the indirect training through D that is also getting updated dynamically.
- The generator G attempts to produce fake examples that are close to the real distribution so as to fool discriminator D.
- The discriminator D tries to decide the origin of the distribution.
- Indirect means that we do not minimize the pixel-wise euclidean distance. The gradients are simply computed from the binary classification of the discriminator.
- The adversarial loss enables the model to learn in an unsupervised manner.
Adversarial Loss
$D$ and $G$ play the following two-player minimax game with value function $ V (G, D) $.
The loss function consists of two parts, the first part is to find $G$ that minimizes $V$ for a given $D$, then, the second part is to find $D$ that maximizes $V$ for a given $G$.
In other words, the adversarial loss can be seperated as the following:
$$ L_D = \frac{1}{M}\sum_{i=1}^{M}[logD(x^i) + log(1 - D(G(z^i)))] $$
$$ L_G = \frac{1}{M}\sum_{i=1}^{M}[logD(G(z^i))] $$
- Minimize G: For the above loss $L_G$, the $logD(X)$ part is a constant. The input for the discriminator is the generated fake data $G(Z)$. In order to fool the discriminator, the expectation of $D(G(Z))$ is expected to be as larger as possible. Therefore, the loss $log(1 - logD(G(Z)))$ is expected to be minimized.
- Maximize D:
- 1st part: The expectation $log(D(X))$ represents that the discriminator input is real data, which is expected to be maximized.
- 2nd part: The $log(D(G(Z)))$ represents that the discriminator input is the generated fake data, which is supposed to be as small as possible, so that the $log(1 - D(G(Z)))$ is expected to be maximized.
Note that, $D$ needs to access both real and fake data while $G$ has no access to the real images.
Training
The framework corresponding to a minmax two-player game should be trained seperately. The training process can be elaborated as the following image.
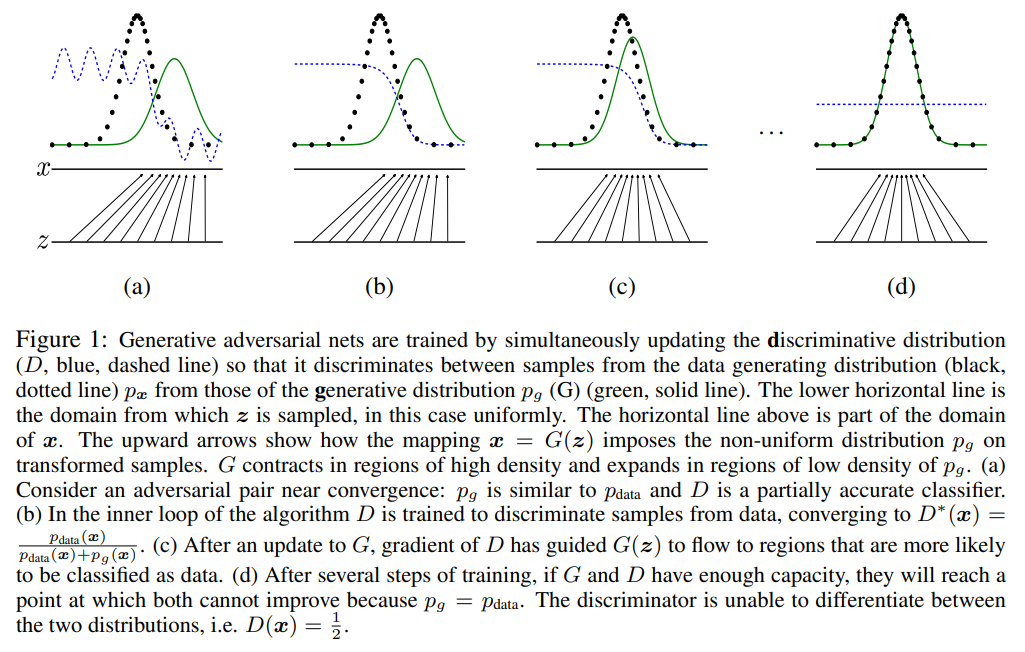
- From (a) to (b), the discriminator is being trained during this process;
- In (C), the generator is being trained to generate more realistic images to fool the discriminator.
- In (d), the distribution of real images and generated data are identical, so that the discriminator’s predicted probability is constantly 0.5.
