Layer Norm | Batch Norm | Instance Norm | Group Norm

LB | BN | IN | GN in NLP

• Batch Norm: Normalizes each feature across the entire batch. Rarely used in NLP, because it relies on consistent sequence lengths and large batch sizes, and is sensitive to padding.
• Layer Norm: Normalizes across the feature dimension for each token independently, making it suitable for variable-length sequences
• Instance Norm: Originally used in computer vision to normalize each channel within each sample. It is not commonly applied in NLP tasks.
• Group Norm: Splits the feature (embedding) dimension into groups and performs normalization within each group. It’s occasionally used in NLP when LayerNorm is replaced for better generalization under small-batch or resource-constrained settings.

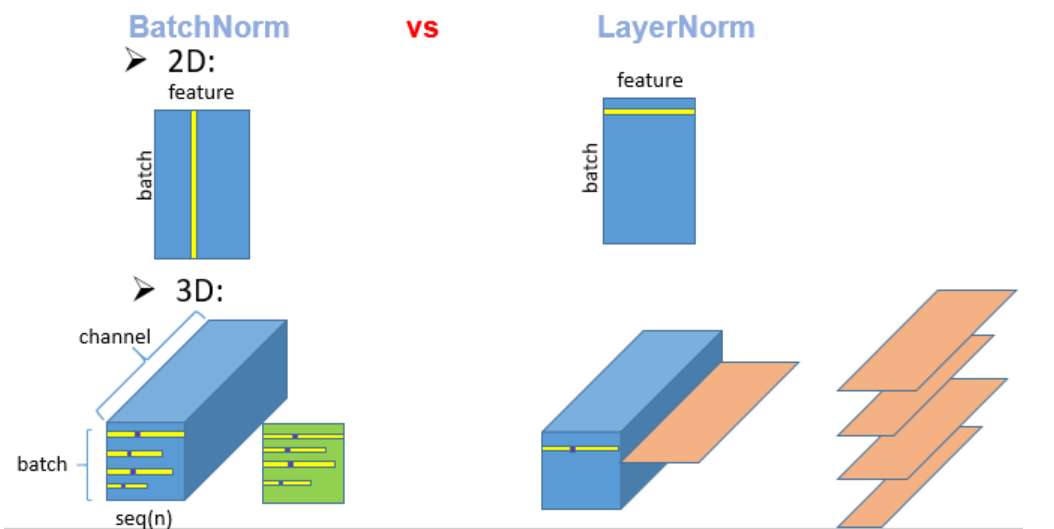
🤖 Scenarios for BatchNorm vs LayerNorm

In terms of operations, BN computes one mean/variance per channel across the entire batch and spatial dimensions, while LN computes mean/variance within each individual sample, across the feature dimension (generally the last dimension dim=-1), independently of other samples and tokens.

• In ML/CV tasks, data often consists of each column representing a feature, and the processed data typically has interpretability, with different units and properties across columns, hence BN is more commonly used in machine learning tasks.
• In NLP, Transformer-based models generally represent data as [batch, seq_len, embedding_dim]. LayerNorm is preferred because it normalizes each token’s embedding independently, preserving token-wise semantics and being robust to variable-length sequences without relying on batch-level statistics.

import torch
import torch.nn as nn

class LayerNorm(nn.Module):
  def __init__(self, emb_dim, eps=1e-5, affine=True):
    super().__init__()
    self.eps = eps
    self.affine = affine
    # scale and shift
    # if affine:
    self.gamma = nn.Parameter(torch.ones(emb_dim))
    self.beta = nn.Parameter(torch.zeros(emb_dim))

  def forward(self, x):
    x_mean = x.mean(dim=-1, keepdim=True)
    x_var = x.var(dim=-1, keepdim=True)
    x_norm = (x - x_mean) / torch.sqrt(x_var + self.eps)
    return self.gamma * x_norm + self.beta

class BatchNorm2d(nn.Module):
    def __init__(self, num_channels, eps=1e-5, momentum=0.1):
        super().__init__()
        self.eps = eps
        self.momentum = momentum
        self.gamma = nn.Parameter(torch.ones(num_channels))
        self.beta = nn.Parameter(torch.zeros(num_channels))
        self.register_buffer('running_mean', torch.zeros(num_channels))
        self.register_buffer('running_var', torch.ones(num_channels))

    def forward(self, x):
        if self.training:
            mean = x.mean(dim=(0, 2, 3), keepdim=True)  # (C,)
            var = x.var(dim=(0, 2, 3), unbiased=False, keepdim=True)
            self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * mean.view(-1)
            self.running_var = (1 - self.momentum) * self.running_var + self.momentum * var.view(-1)
        else:
            mean = self.running_mean.view(1, -1, 1, 1)
            var = self.running_var.view(1, -1, 1, 1)

        x_hat = (x - mean) / torch.sqrt(var + self.eps)
        return self.gamma.view(1, -1, 1, 1) * x_hat + self.beta.view(1, -1, 1, 1)

🧠 Summary Comparison: BatchNorm vs LayerNorm

Feature	BatchNorm	LayerNorm
Depend on batch size?	✅ Requires cross-sample statistics	❌ Independent of batch size
Handles variable-length sequences?	❌ Padding affects statistics	✅ Each token is normalized independently
Inference stability?	❌ Uses moving average, can be unstable	✅ Consistent behavior during inference
Multi-GPU / small batch stability?	❌ Very unstable	✅ Not affected at all
Suitable for Transformer architecture?	❌ Breaks token-wise independence	✅ Perfectly matches token-wise design

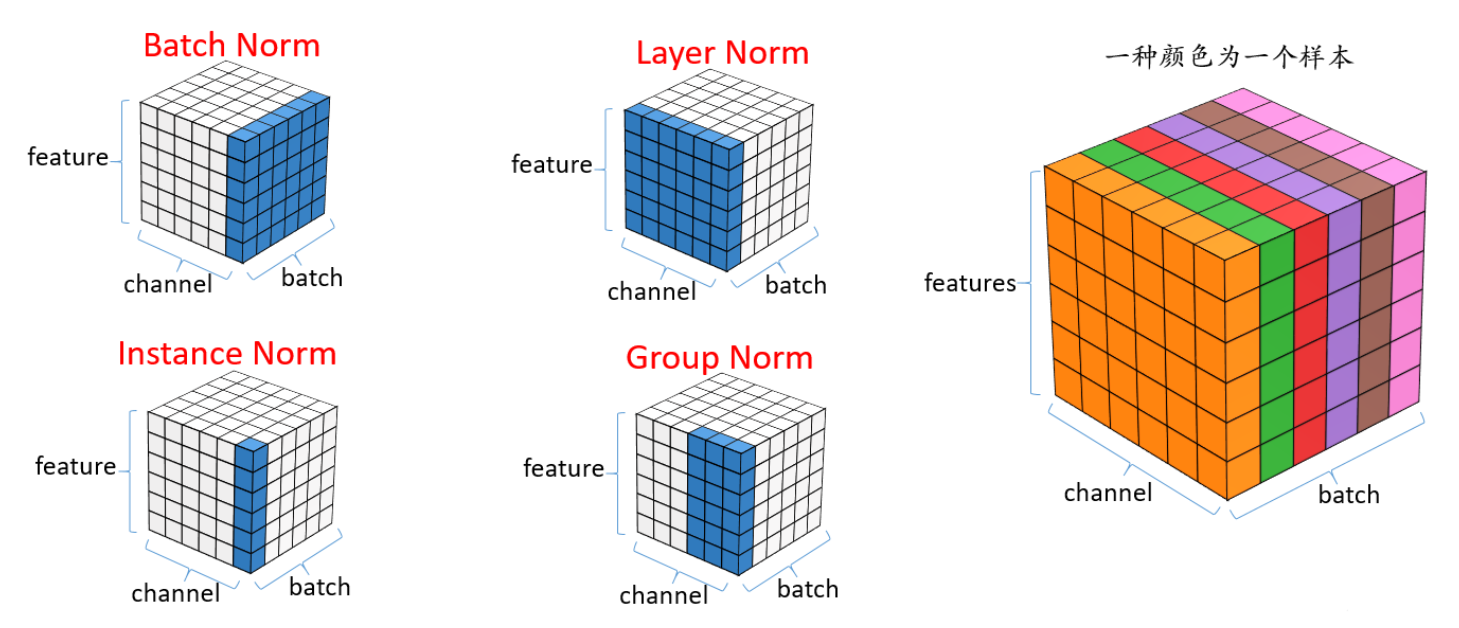
LB | BN | IN | GN in CV

Considering feature maps with shape (N, C, H, W):

• N: batch size
• C: number of channels
• H, W: spatial dimensions

Different normalization methods apply statistics over different dimensions:

• Batch Norm (BN): Normalizes each channel using statistics computed across the batch (N) and spatial dimensions (H, W). Each channel shares a single mean and variance across all samples and locations.

• Layer Norm (LN): Normalizes across all channels and spatial dimensions within each sample, making the entire feature map of a sample zero-mean and unit-variance.

• Instance Norm (IN): Normalizes each channel independently per sample, using only the spatial dimensions (H, W) of that channel.

• Group Norm (GN): Divides channels into groups (e.g., 32 groups), then normalizes the features within each group across spatial dimensions, per sample.

🤖 Scenarios for Instance Norm and Group Norm:

• Instance Norm: it is particularly suited for style transfer tasks and image generations. Instance normalization helps maintain the individuality and unique style of each image, free from batch-level interference.
• Group Norm: Particularly effective in scenarios with small batch sizes or batch size = 1, such as object detection and image segmentation. By normalizing over groups of channels within each sample, it provides stable training dynamics and better generalization where BatchNorm may fail.

class InstanceNorm(nn.Module):
  def __init__(self, num_channels, eps=1e-5, affine=True):
    super().__init__()
    self.eps = eps
    self.affine = affine
    self.gamma = nn.Parameter(torch.ones(num_channels))
    self.beta = nn.Parameter(torch.zeros(num_channels))

  def forward(self, x):
    x_mean = x.mean(dim=(2, 3), keepdim=True)
    x_var = x.var(dim=(2, 3), keepdim=True, unbiased=False)
    x_norm = (x - x_mean) / torch.sqrt(x_var + self.eps)
    return self.gamma.view(1, -1, 1, 1) * x_norm + self.beta.view(1, -1, 1, 1)

class GroupNorm(nn.Module):
  def __init__(self, num_groups, num_channels, eps=1e-5, affine=True):
    assert num_channels % num_groups == 0
    self.num_groups = num_groups
    self.num_channels = num_channels
    self.eps = eps
    self.affine = affine
    self.gamma = nn.Parameter(torch.ones(num_channels))
    self.beta = nn.Parameter(torch.zeros(num_channels))

  def forward(self, x):
    Batch, Channel, Height, Width = x.shape
    x = x.view(Batch, self.num_groups, -1)
    x_mean = x.mean(dim=-1, keepdim=True)
    x_var = x.var(dim=-1, keepdim=True, unbiased=False)
    x_norm = (x - x_mean) / torch.sqrt(x_var + self.eps)
    x_norm = x_norm.view(Batch, Channel, Height, Width)
    return self.gamma.view(1, -1, 1, 1) * x_norm + self.beta.view(1, -1, 1, 1)

References ⭐

• 归一化方法 BN、LN、IN、GN、SN
• Normalization之BN, LN, IN, GN